|
||||
| Anfoworld に戻ります。 | ||||
 |
|||||||
|
|||||||
|
 |
||||||
|
||||
| Anfoworld に戻ります。 | ||||
 |
|||||||
|
|||||||
|
 |
||||||
|
|||||


|
||||
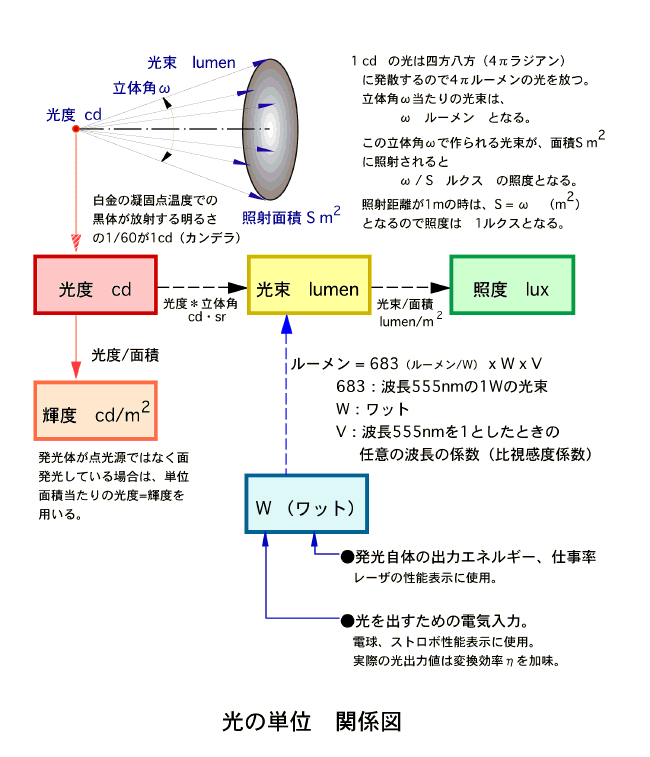
| 『1気圧(101,325ニュートン/m2 )のもとで完全黒体を加熱し、白金の融けだす温度(凝固点温度 = 2042K)になった時、1cm2 の平らな表面から放射される光の中の垂直方向の明るさの1/60』 | |||
|
|||
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
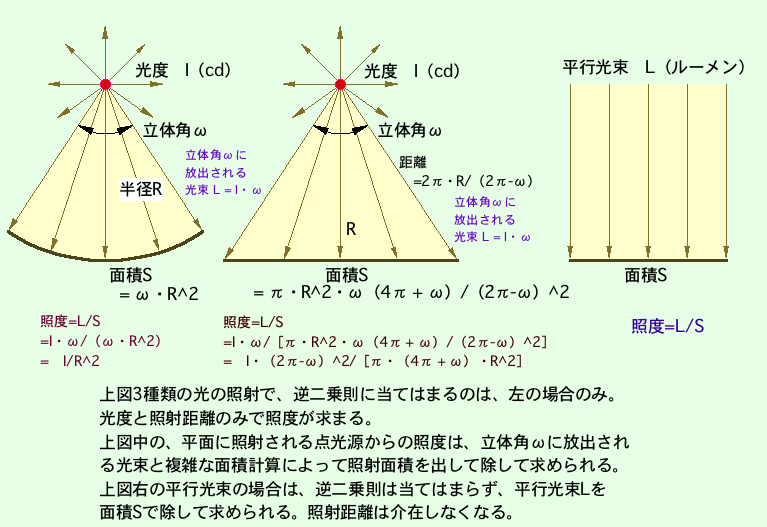
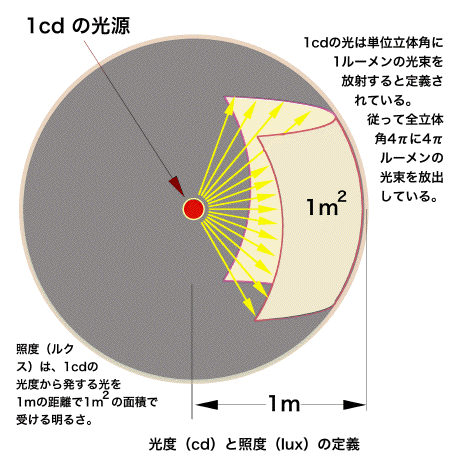 照度(Lux = ルクス)は、我々の生活の中で明るさを表す数値として一番馴染みの深い単位です。
照度(Lux = ルクス)は、我々の生活の中で明るさを表す数値として一番馴染みの深い単位です。
| 1カンデラの光度を持つ点光源(すなわち4πルーメンの光束を放つ光源)が1メートルの距離から照射した明るさを1ルクスとする。 | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
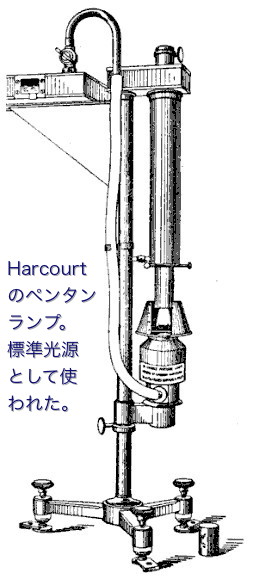
 フランス生まれのドイツの哲学者、数学者。
フランス生まれのドイツの哲学者、数学者。
 燭は、光の単位である『光度』の古い言い方です。
燭は、光の単位である『光度』の古い言い方です。
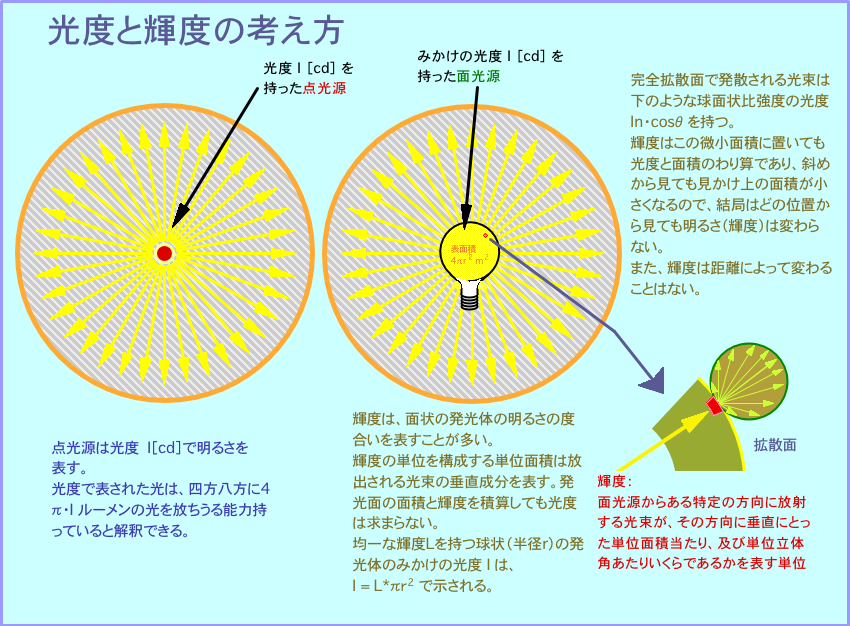
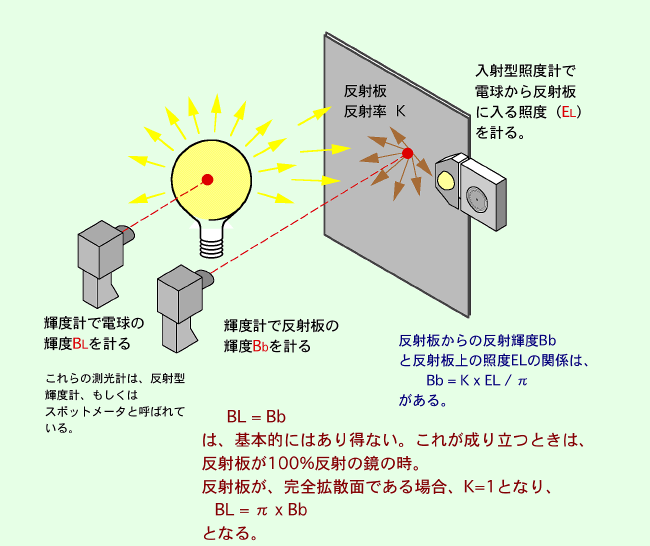
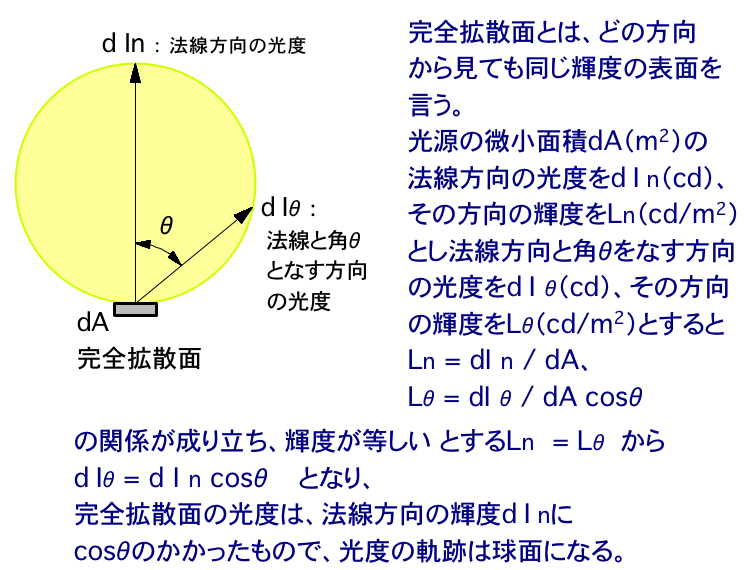
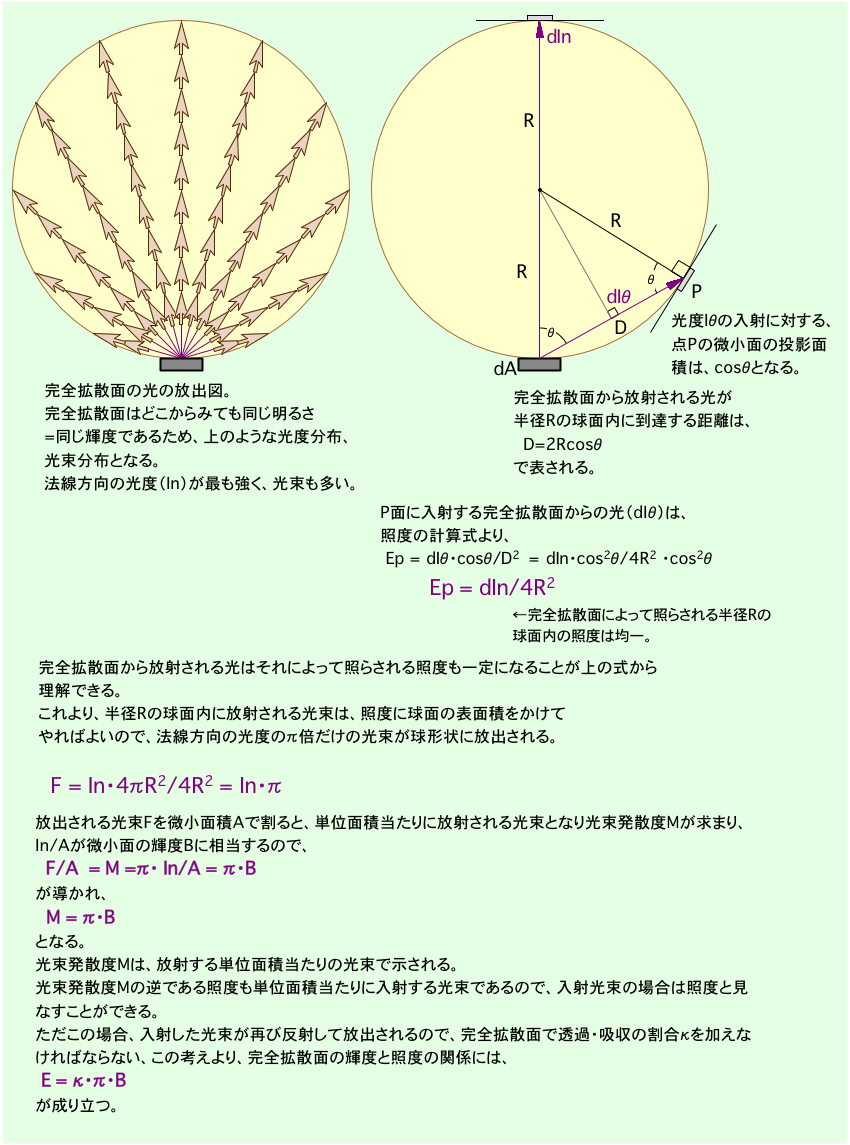
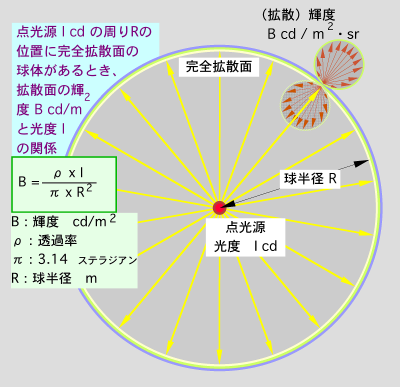 光度I(cd)を持った点光源の周りを拡散板で覆った場合、拡散板の輝度 B(cd/m2)がどのようなものになるか検討して見ましょう。
光度I(cd)を持った点光源の周りを拡散板で覆った場合、拡散板の輝度 B(cd/m2)がどのようなものになるか検討して見ましょう。
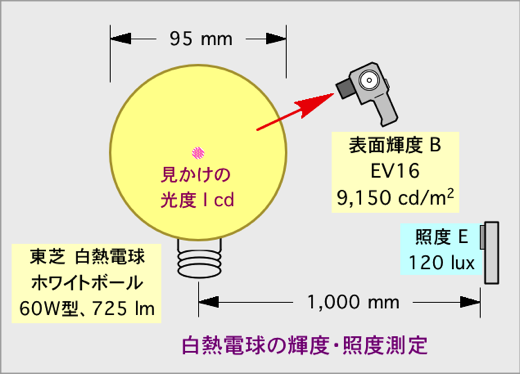 ということがわかります。
ということがわかります。